Robbie Hatley's Solutions, in Perl, for The Weekly Challenge #350 (“Good Substrings” and “Shuffle Pairs”)

For those not familiar with "The Weekly Challenge", it is a weekly programming puzzle with two parts, with a new pair of tasks each Monday. You can find it here: The Weekly Challenge

The Weekly Challenge for the week of 2025-12-01 through 2025-12-07 is #350. The tasks for challenge #350 are as follows:

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Task 350-1: Good Substrings
Submitted by: Mohammad Sajid Anwar
You are given a string. Write a script to return the number of
good substrings of length three in the given string. A string is
good if there are no repeated characters.

Example #1:
Input: $str = "abcaefg"
Output: 5
Good substrings of length 3: abc, bca, cae, aef and efg

Example #2:
Input: $str = "xyzzabc"
Output: 3
Good substrings of length 3: "xyz", "zab" and "abc"

Example #3:
Input: $str = "aababc"
Output: 1
Good substrings of length 3: "abc"

Example #4:
Input: $str = "qwerty"
Output: 4
Good substrings of length 3: "qwe", "wer", "ert" and "rty"

Example #5:
Input: $str = "zzzaaa"
Output: 0

Given string $s, I'll iterate "for my $idx (0..$n-3) {}", where $n is length, and consider the current, next, and next-next characters, and if they're all different I'll increment a counter $c (which starts at 0). Then just return $c.

Robbie Hatley's Perl Solution to The Weekly Challenge 350-1

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Task 350-2: Shuffle Pairs
Submitted by: E. Choroba
If two integers A <= B have the same digits but in different
orders, we say that they belong to the same shuffle pair if and
only if there is an integer k such that B = A * k where k is
called the witness of the pair. For example, 1359 and 9513
belong to the same shuffle pair, because 1359 * 7 = 9513.
Interestingly, some integers belong to several different shuffle
pairs. For example, 123876 forms one shuffle pair with 371628,
and another with 867132, as 123876 * 3 = 371628,
and 123876 * 7 = 867132. Write a function that for a given $from,
$to, and $count returns the number of integers $i in the range
$from <= $i <= $to that belong to at least $count different
shuffle pairs.

PS: Inspired by a conversation between Mark Dominus and
Simon Tatham at Mastodon.

Example #1:
Input: $from = 1, $to = 1000, $count = 1
Output: 0
There are no shuffle pairs with elements less than 1000.

Example #2:
Input: $from = 1500, $to = 2500, $count = 1
Output: 3
There are 3 integers between 1500 and 2500 that belong to
shuffle pairs.
1782, the other element is 7128 (witness 4)
2178, the other element is 8712 (witness 4)
2475, the other element is 7425 (witness 3)

Example #3:
Input: $from = 1_000_000, $to = 1_500_000, $count = 5
Output: 2
There are 2 integers in the given range that belong to 5 different
shuffle pairs.
1428570 pairs with 2857140, 4285710, 5714280, 7142850, and 8571420
1429857 pairs with 2859714, 4289571, 5719428, 7149285, and 8579142
The witnesses are 2, 3, 4, 5, and 6 for both the integers.

Example #4:
Input: $from = 13_427_000, $to = 14_100_000, $count = 2
Output: 11
6 integers in the given range belong to 3 different shuffle pairs,
5 integers belong to 2 different ones.

Example #5:
Input: $from = 1030, $to = 1130, $count = 1
Output: 2
There are 2 integers between 1020 and 1120 that belong to at least
one shuffle pair:
1035, the other element is 3105 (witness k = 3)
1089, the other element is 9801 (witness k = 9)

I tried the approach of calculating all permutations of all numbers, but the run times were in the weeks, so I had to abandon that approach.

Instead, I now use the method of "digit signatures" (the digits in ascending order). The decimal expansions of two positive integers will be permutations of each other if-and-only-if they have the same signature.

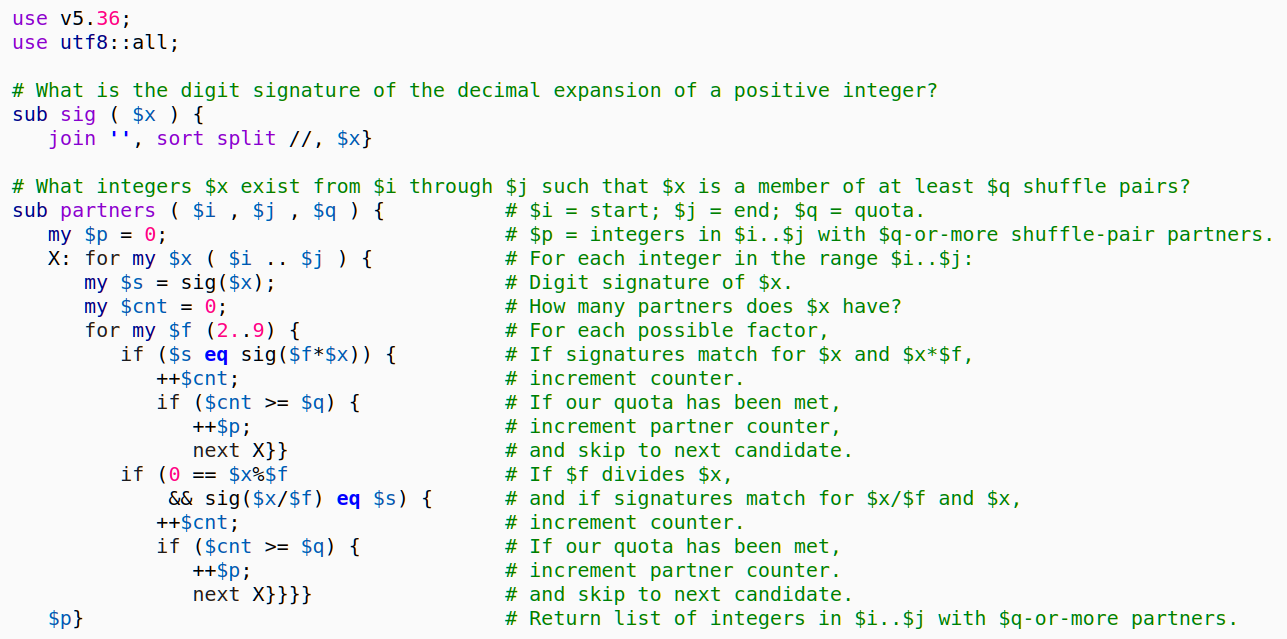
Robbie Hatley's Perl Solution to The Weekly Challenge 350-2

That's it for challenge 350; see you on challenge 351!